在Zemax中使用几何射线追踪来获得衍射受限的结果,提出了一个必须予以克服才能正确地对现实系统建模的挑战。
ZEMAX中的激光源定义方法,支持运用光线追踪进行现实系统建模。
Alexander Brodsky 和 Natan Kaplan
HOLO/OR
关键词:光学设计,多模激光,部分相干,BSDF,ZEMAX,光束质量因子,M2。
摘要
在默认情况下,光学系统通常是专为单模激光设计的系统。尽管如此,许多工业激光器的M2在3到大约100的范围内,通常被称为“多模”或“部分相干”激光器。这些激光源包括多模光纤激光器、多模光纤耦合二极管激光器、准分子激光、多模固态激光器和VCSEL阵列。虽然M2激光器在聚焦能力方面存在一些缺点,但与单模激光器相比功率更高,并且对系统中光学元件的精度要求更低。遗憾的是,作为最常见的建模软件工具之一,Zemax™没有提供一种标准的方法来对于顺序模式下的多模激光器进行建模,因此迫使大多数设计人员为单模源进行设计,然后试图通过近似值来解释多模效应。即使在为单模激光器设计时,光线跟踪往往会在感兴趣的地方(如焦面透镜)产生不真实的结果。
通过应用一种散射模型,本文讨论了一种在Zemax中模拟和优化单模和多模激光器的新方法。这一概念允许人们使用几何光线跟踪来实现类似物理光学的结果,包括镜头焦点处的实际光斑尺寸,同时仍然快速简单地进行系统优化。
我们将首先讨论激光的性质和M2的定义。其次,我们演示了用于光线跟踪模拟的新散射模型方法,并显示了结果。在最后一部分,我们提出了具体的案例研究,以显示该方法的有效性和局限性。
1. 简介
任何激光束都可以用三个参数来描述:波长、振幅(或强度)空间分布和相位(或波前)空间分布。单模激光束的独特性质是在束腰部位置具有高斯振幅和零相位差。多模激光束具有任意的振幅和相位。
激光束的光束质量(或光束的“多模”状态)通常由M2项定义。这是一个简化的数字,它考虑了所有三个激光参数,并重新定义了光束大小和光束发散度,而不是振幅和相位。在图1中,我们显示了统计上M2相同的一些相位和振幅分布图的示例。假设波长是恒定的,可以通过更改光束大小和发散度来改变激光器的M2。
为了更好地理解M2,我们考虑两种情况:单模高斯光束,随后是理想负透镜与光学扩散器。在这两种情况下,光束的发散度和束腰处的直径可以相等,但是对于第一种情况,光束保持为单模,对于第二种情况,光束变成多模。对此的解释是,对于第一种情况,我们可以通过放置一个正透镜,很轻松地减去透镜的波前相位相加,激光将完全变回单模状态。从数学上来说,我们也可以对第二个示例进行同样的操作,但是实际上,要找到消除散射效应的准确波前逆相位要复杂得多。
那么,“多模激光束”的定义是否与利用先前关于激光束的知识找到一个合适的校正方法,然后将其转换为单模光束的容易程度有关呢?我们会说“是”,至少部分有关。
通过利用这一见解,我们可以看到,M2对光学系统性能的一般影响可以通过“不可重构”的任何波前相位相加来建模,即不与系统中的光学组件共享任何对称性。
光学设计工具具有很好的覆盖范围,可用于使用几何光线跟踪进行建模和优化。物理光学的工具开发较少,并且在限制计算机内存和时间消耗方面面临极大挑战。因此,建模M2的最佳解决方案是找到一种使用几何光线跟踪内核来解决与物理光学相关的问题(例如,光的复波表示)的方法。在下一节中,我们提出了一些实现这一目标的想法,基于这样的见解,即射线源必须创建不可重建的射线分布。
2. 基于几何光线追踪的多模光束仿真建模:
其基本理念是,应用一种与光学系统内所有其他光学部件不相关的波前形状。例如,如果光学设置中的所有光学部件均为棱镜,则可以通过施加球面波前来建模多模激光源。在光学设置基于透镜的情况下,则对于多模激光器,可以使用具有棱镜光焦度的波前,例如棱镜阵列。棱镜阵列或透镜阵列是通用解决方案,适用于大多数激光系统,但具有多个阵列的系统除外。但是,由于控制单个光线的复杂性和有限的几何选项,一些使用阵列的标准优化方法变得不够。因此,数组不是一个好的建模选择。
我们正在寻找一种特殊的波前,它的几何形状不能用笛卡尔坐标的形式或径向对称来描述。
一种选择是使用方位对称性的波前。其中最著名的示例是螺旋相位板(SPP)或涡旋相位片[1],[2],[3]。该功能广泛用于产生高斯-拉盖尔高次模。光束的M2可以通过螺旋相位板(SPP)的光学功率来控制,表现为沿方位角坐标的累积弧度。在图2中,示出了与不同M2值相关的具有不同光学功率的螺旋相位板(SPP)方位角波前。
这种方法与不交轴光线的方法有些相似。[4],[5]与不交轴光线不同,方位角方法具有物理意义,不需要进行初步计算,可以与大多数分析和优化工具一起使用。
另一个选择,也就是我们在本文中使用的方法,通过使用BSDF [6],[7]全散射式方法对多模效应进行建模。它最初并非专为该任务创建,但根据定义,在预定义的配置中,重定向几何射线的散射概念与所有其他光学表面不相关,这使得它适合于使用。Holo/Or 已经使用这种方法来开发 M2 变换模块,其中将M2 变形重组为两个正交坐标[8],[9]。此外,还进行了实验验证,证实了这一点[10]。在示例中,我们将集中讨论这种散射方法。
3. 设计示例
3.1 Zemax™中的初始设置定义
与任何激光光学系统设计一样,我们从定义常规属性开始-波长、光圈值、镀膜类型和镀膜因子。
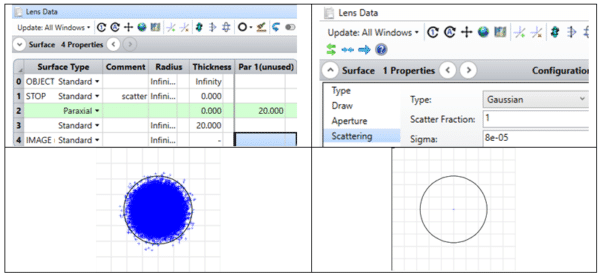
高斯镀膜型的镀膜因子将被定义为1,因为稍后将通过散射到Airy磁盘中来调整发散度。接下来,插入一个标准曲面,在属性选项卡中,选择散射,然后选择一种特定的散射方法来描述角度光线的分布和角度。本文采用高斯散射类型将散射分数设置为1。然后在开放光斑图上修改光线散射的西格玛值,使光斑图中的光线充满Airy磁盘。该西格玛值对应于单模M2 =1。
为了定义不同的M2值,我们将M2=1的西格玛值乘以我们想要建模的M2值(例如,我们将西格玛乘以10的因子来建模M2=10)。
在图3左上方,我们显示了简单设置的透镜数据编辑器,其中包括近轴透镜和右上方的散射窗口的界面。图3左下方显示调整发散度以填充Airy磁盘的光斑图,右下方参考光斑图没有显示增加散射。我们看到,如果没有散射,所有的光线都会到达单个几何点,而不会描述真实的光斑大小。
在下一节中,我们回顾一些案例研究,以展示模型的正确性和使用它的好处。
3.2 通过近轴透镜聚焦M2值为 1和10的单模激光束
在这里和接下来的示例中,我们使用了Holo/Or的光学计算器。
首先,证明模型与理论值一致很重要。为此,我们将比较束腰和距离束腰的瑞利长度处的波束大小,已知比率为 √2
模拟参数:波长1064纳米,光束直径6mm,EFL 20mm,切角因子4,孔径尺寸12mm。
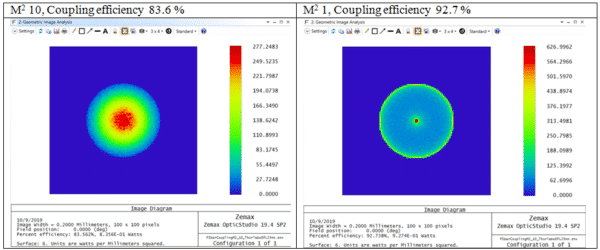
在图4中,我们在ZX平面上显示了2D强度图,以显示新的焦点尺寸。白色虚线是理论上的光斑尺寸,绿色虚线与模拟光斑的尺寸相关。单模M2=1(左图)和多模M2=10(右图)的理论值和模拟值之间的计算差值小于2 %,对于大多数应用来说,这已经足够接近了。
3.3 使用标准三重态耦合器进行光纤耦合
为了进行光纤耦合效率分析,我们选择了Thorlabs的三重准直器模型(TC25 APC-1064–1060nm,f=25.23 mm,NA=0.25,FC/APC)。为了进行模拟,我们使用相同的直径为6 mm的入射光束,其中M2=10,由散射定义,波长为1064纳米。任务是检查NA 0.22和纤芯0.1 mm光纤的耦合效率。对于位置优化,我们使用了IMAE操作数。
3.4 空气间隔双分透镜和单透镜用于聚焦的比较
高多模光源对光学质量的敏感性较低,因为强光束质量的光学效应掩盖了光学缺陷。这些知识有助于在不必要的地方节省光学质量方面的投资。
在本例中,我们继续使用相同的输入参数,并将Thorlabs目录中由高折射率玻璃(型号ACA254-030-1064)制成的空气间隔双合透镜与一个简单的平凸透镜进行比较。两个聚焦元件的物镜焦距(EFL)均为30mm。调整因子设置为2.25,这对于高功率聚焦应用来说,通常用于防止孔径减小。
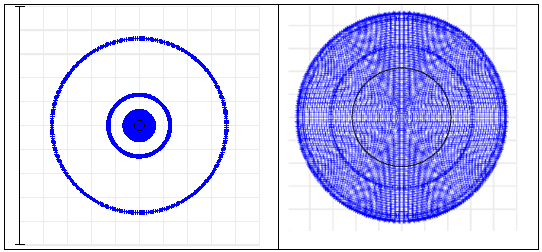
在图6中,我们显示了单模高斯源的光斑图。左图为单重态,右图为双重态。根据光线相对于Airy磁盘(黑线圆)的分布,双合线态的性能比单合线态更好(像差更小)。
在接下来的图7中,我们显示了M2=1(左)和M2=10(右)的光束的几何图像分析。
对于M2=1,具有双合透镜的光斑看起来很好,并且相对于单模激光的衍射极限,光斑尺寸仅增加了20 %,但是对于单合透镜,光斑尺寸几乎是衍射极限的4倍。对于M2=10,情况则完全不同 – 双态和单态的结果完全相同。在这种特殊情况下,当使用多模式激光器时,每台设备的经济性价格可达数百美元。
*ZEMAX对于多模式耦合有自己的教程场景[11]。光束模型中的散射概念已在此教程场景中得到了证实。
4. 综述与结论:
我们提出了一种使用带有附加角度散射的几何射线跟踪对真实光束建模的方法,以沿整个光路获得真实的光束尺寸值。该方法特别适用于多模激光器光学系统的设计。由于是几何形状,我们的方法在开发时间上比物理光学方法具有很大的优势,可以用于任意多模光束。对于时间相干性、干涉和衍射效应很重要的情况,该方法具有局限性。
为了展示散射方法的功效,我们展示了几个基本示例,其中将该方法用于散焦分析、光纤耦合效率估计以及光斑大小和形状的模拟。
在大多数情况下,高M2的多模激光器可以接受像差更高的光学元件。
参考文献:
- Wang, Xuewen等人。“光学涡旋产生的最新进展” 。纳米光子学7.9 (2018年):1533-1556.
- Tian, Ya-Li等人“亮光阱和暗光阱中单中性原子的量子比特的比较”。《中国物理》B 28.2(2019年):023701。
- Tiferet, Maor等人。“基于超分辨成像技术的硅的等离子体色散效应”。生物医学应用的纳米量级的成像、传感和驱动XVI。第10891卷。国际光学和光子学学会,2019年。
- Zhang, Shuhe, Jinhua Zhou 和 Lei Gong。“非傍轴高斯光束的不交轴光线模型”。《光学快报》26.3 (2018年):3381-3393。
- Colbourne, Paul D.“通过使用不交轴光线一般象散高斯光束的表达和优化”国际光学设计会议。美国光学学会,2014年。
- Asmail, Clara.“双向散射分布函数(BSDF):系统化的参考书目”。国家标准技术局研究杂志96.2(1991年):215.
- OpticStudio可提供哪些散射模型?https://my.zemax.com/en-US/Knowledge-Base/kb-article/?ka=KA-01415.
- Brodsky, Alexander和Natan Kaplan。“极坐标旋转系统中变形光束整形的解析和实际运用”光学及激光技术杂志107 (2018年):408-414.
- LeanLine https://www.holoor.co.il/products/leanlinetm.
- Brodsky, Alexander和Natan Kaplan。“极坐标中变形M 2激光相变的实验演示”。光学工程58.6 (2019年):065106.
- 多模光纤耦合https://my.zemax.com/en-US/Knowledge-Base/kb-article/?ka=KA-01351.
此条目被翻译成中文。对于原文条目,请将语言改为英语。